|
|
Structure of Magic and Semi-Magic Squares, Methods and Tools for Enumeration |
by Francis Gaspalou |
|
Order 4 allows to compute easily the set of magic (or semi-magic) squares. Then you can handle this set for examination and you have a lot of results on the structure. For orders superior to 4, it is practically impossible to handle the set: the squares are too numerous or can't be computed.
The 32 transformations of a given magic square of order 4 can be obtained as follows:
With the matricial notation, these 32 transformations are:
These notations are personal notations. You have a set of 32 elements:
1 element of period 1: I,
19 elements of period 2: V, H, G, D, R2, IT, EX, M, N, X, Y, A, V*A, H*A, G*A, D*A, R2*A, Z*A, T*A, 12 elements of period 4 (all with a common square R2): R1, R3, Z, T, R1*A, R3*A, IT*A, EX*A, M*A,
N*A, X*A, Y*A.
It is possible to build a multiplication table and to demonstrate in that way you have a group. The relations of definition ("abstract definition") allows a smarter demonstration. You have nevertheless to proceed by trial and error to find the good relations of definition among the 51 possible groups of order 32! The literature does not give exhaustive catalogues, only partial catalogues and for low orders. When you take
s1 = R1, s2 = X*A, s3 = IT, s4 = G,
you find that all the relations of definition of group G 32 n° 7 of BURNS are verified [Reference: Josephine E. BURNS, The Abstract Definitions of Groups of Degree 8, Am. J. Math. 37 (1915), p. 207]:
Besides, you verify that the 4 generators R1, X*A, IT et G give 32 elements. Therefore, the 32 transformations form a group: the group G 32 n° 7 of BURNS. The 8 first transformations form the octic group D4. The 16 first transformations form the group D4*C2. It is the group n° 4 of BURNSIDE among the 9 not abelian groups of order 16 [Reference: W. BURNSIDE, Theory of Groups of finite order, Dover 1911, p.146]:
P4 = E, Q2 = E, R2 = E, R-1PR = P3, P-1QP = Q, R-1QR = Q
You can verify it easily with P = R1, Q = IT, R = G It is the direct product of {Q} by {P,R}.
We can calculate the order of the group G for magic squares of order n. For magic squares of order 4, we have seen that group G is of order 32. It is the product of 8 (order of group octic) by 4 (number of remaining transpositions). In magic square language, we call transpositions permutations of rows and columns symmetrically located from the centre of the square (it is not the usual mathematical language for permutations). If the rows are called 1234, we see there are 8 transpositions:
We search permutations abcd such as a+d=b+c=5
Among these transpositions, the transposition 4321 is already in the octic group: it is the transformation R2 (symmetry about the centre).
It is sufficient to fix a and b: a can take 4 values, and b=2 values when a is given. Then we have 4*2=8 solutions Therefore, 32 is the product:
8*(number of transpositions /2) = 4*(number of transpositions)
This formula can be generalized for all the orders. For order 6, the number of transpositions abcdef is 6*4*2=48
a can take 6 values, b can take 4 values when a is given, c can take 2 values when a and b are given, d=7-c, e=7-b, f=7-a.
Then the order of group G is 4*48 = 192.
For order 2p, the number of transpositions is 2p*(2p-2)*...*2=2p (p!) and the order of group G is 4*2p (p!) = 2p+2 (p!). We have the fundamental result: for magic squares of order 2p, the order of group G is 2p+2 (p!) We see easily that for magic squares of order 2p +1, the order of group G is the same: 2p+2 (p!).
As a matter of fact, the number of transpositions is the same as for order 2p (the middle number doesn't move).
These two groups are isomorphic; they have the same abstract definition. Therefore, for magic squares of order n=2p or n=2p+1, the order of group G is 2p+2 (p!). This last formula seems original. The first values are:
Note: for semi-magic of order n, the order of group G is 2 (n!)2.
The demonstration is here obvious: for a given square, you have n! possible permutations of rows, idem for columns, therefore (n!)2 possible transformations and you double this number with symmetry about the first diagonal.
This set is defined for example by A1+A2+B1+B2=34 (it is not the only definition: you can have also A2+B1+C4+D3=34 or A1+A3+C1+C3=34, etc.). 3.1 Group G
The group G (transformations) is of order 1 152; you have 3 elementary squares. I identified this group: it is the only group of order 1 152 of degree 8 (reference: J. BURNS's article already quoted). Its abstract definition is:
with for example
You can verify that all the relations of definition are true with these two generators (and you need to verify also that you have 1 152 generated elements: these relations aren't abstract definition of a subgroup). This group has a large number of subgroups (non exhaustive list, notations of J. BURNS's article if any else indication) - it is a mine! -:
G 576 n° 1, 2, 3
For each subgroup, the abstract definition is in the literature and I can give example of generators.
G 288 n° 3 G 192 n° 1, 2 G 144 n° 1 G 128 G 96 n° 3, 4, 6 G 72 degree 6 G 64 n° 2, 3, 5 G 48 n° 1 G 32 n° 6, 7, 8, 9 G 24 degree 4 G 16 n° 1 (?), 9 G 8 (octic group) and its subgroups. I think G 1 152 has not subgroup of order 384. 3.2 Group G'
The group G' (permutations) is of order 384; you have 9 elementary squares. This group is G 384 degree 8. Subgroups (non exhaustive list):
G 192 n° 4, 5
G 128 and its subgroups (the same as above). G 1 152 and G 384 have G 128 as a common subgroup (with also all its own subgroups). 3.3 Decomposition
The set of 3 456 semi-pandiagonal squares is made with 9 types of squares:
Note: I put a double frame in a type diagram and a simple frame in a transformation diagram. Each type has 384 squares and a group structure. There are the 6 DUDENEY's types I, II, III, IV, V, VI (IV and IV' are the same type for DUDENEY; idem for V and V'; idem also for VI and VI'). It is funny to identify the transformations between the 9 types of squares (internal transformations for some types, but external transformations for other types). With these external transformations, you see that the 9 sets of 384 squares are isomorphic. Note you have 2 supplementary isomorphic sets with 384 squares: they are of DUDENEY's type VI. These 768 squares aren't semi-pandiagonal. They can be defined - for example - as squares of DUDENEY's type VI with condition A2+B4+C1+D3=34 or A3+B1+C4+D2=34.
You have 1 152 squares with condition A2+B4+C1+D3=34 or A3+B1+C4+D2=34: the 384 symmetrical squares and the 2 supplementary sets above.
3.4 Intermediate Square
All the 3 456 semi-pandiagonal squares can be built with only one intermediate square. For example, you can take (cf. BENSON & JACOBY, page 111):
This intermediate square is a Greco-Latin square: it is magic, diagonal (see definition in The intermediate square method, § 4) and semi-pandiagonal. You have no magic conditions. You have 4! =24 solutions for capital letters, 4! solutions too for lower-case letters, k=6 basis; therefore you have a set of 6*24*24 = 3 456 squares. This demonstration is simplier than BENSON & JACOBY'.
For magic squares of order 4, you find the following graph of filiation: 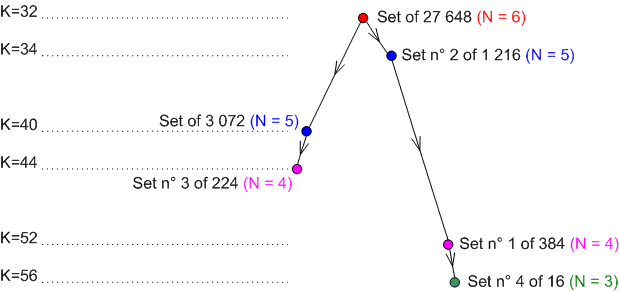
K is the number of magic series (relations a+b+c+d = 34). Cf. The transformation method, § 5.1. The origin set of 27 648 squares is the set of semi-magic squares of DUDENEY's type VI, i.e. defined by the 3 conditions:
The set n° 2 of 1 216 squares is the set of 27 648 semi-magic squares with condition:
A1+B2+C3+D4=34 (and D1+C2+B3+A4=34 which is a consequence of DUDENEY's type VI)
The set n° 1 of 384 squares is the set n° 2 of 1 216 squares with condition of semi-pandiagonal squares:
A1+A2+B1+B2=34 for example (and other induced relations).
This set n° 1 is the set of semi-pandiagonal squares of DUDENEY's type VI. The set of 3 072 squares is the set of semi-magic squares of DUDENEY's type IX.
It is also the set of 27 648 semi-magic squares with condition:
D1+B2+B3+D4=34 (and other induced relations) given by transformation
The set n° 3 of 224 squares is the set of 3 072 squares with magic conditions for the diagonals (and with other induced conditions).
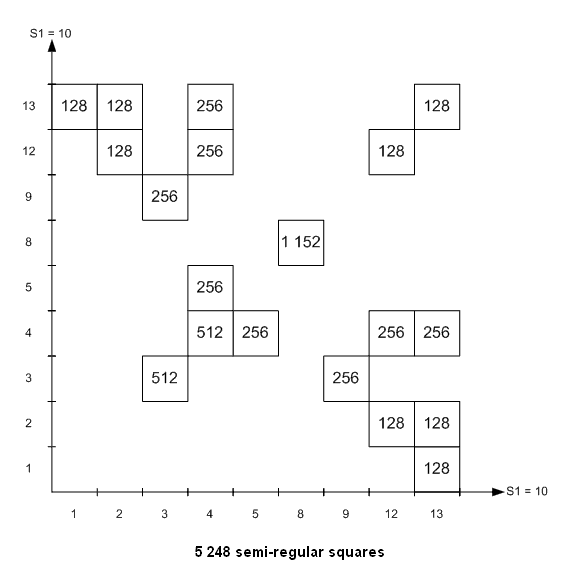
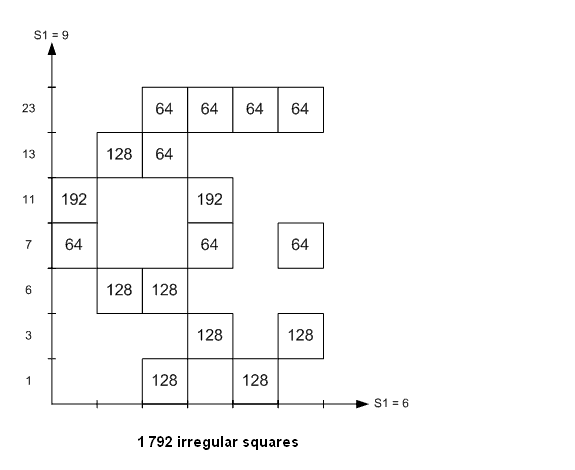
For order 4, it is possible to show exactly how the 7 040 magic squares are generated from capital and lower-case letter squares. For that, it is not necessary to enumerate all the possible Gallic squares, you need only to identify the elementary lower-case letter Gallic squares (and the induced squares by group G of 32 and by permutations). You search after the orthogonal squares to these elementary Gallic squares. You have to search only Gallic squares with semi-regular rows and columns because only diagonals can be irregular (you verify this property a posteriori on all the 7 040 squares and all the basis; maybe it is possible to demonstrate directly that rows and columns cannot be irregular). If you classify the Gallic squares according to the value of the parameter S1, sum of the first diagonal, you verify on the 7 040 squares that S1 can take only some values (then the sum of the second diagonal is S2=2σ-S1). And among these Gallic squares, you have to take only those which have orthogonal squares. I give hereafter the result of my research. With the first basis (1,2,3,4;0,4,8,12), I found:
For each elementary square, I searched the number of induced squares and the number of orthogonal squares:
(There are 80 Latin magic squares, coming from the elementary squares # 1, 2, 8 and 12.
There are 48 Latin diagonal squares coming from the elementary square # 8. You see that Latin magic squares haven't the maximum number of orthogonal squares. The total number of orthogonal squares to Latin magic squares is 2 048 - with 1 152 orthogonal to Latin diagonal squares - ).
Then, I built two figures: one for the 5 248 semi-regular squares and another for the 1 792 irregular squares:
The 7 040 magic squares are distributed in blocks of squares. In each block, all the squares come from the same couple of two elementary Gallic squares, each one in a normalized position. In fact, for the capital letters values (0,4,8,12), I used the same program as for lower-case letters values (1,2,3,4) with: 0→1 4→2 8→3 12→4
In that way, the Gallic squares are written in a normalized form.
The figures give the number of magic squares in each block, but naturally I identified each magic square in the list of 7 040. All the 7 040 magic squares can be built from 9+6+7=22 elementary Gallic squares (with the first basis). I also drove the decomposition of the 7 040 squares with the second and the third basis (with the 3 other basis, the diagrams are obtained by permutation of capital and lower-case letters, i.e. by symmetry about the first bisecting line). I give the results:
The set of 1 152 regular squares is different in the 3 basis. The 3 sets of 1 152 constitute the set of 3 456 semi-pandiagonal squares. There are 4 224 squares which are always semi-regular in all the basis and 1 280 squares which are always irregular in all the basis. There are 5 760 semi-regular squares with at least one basis. Note: for orders superior to 4, it is naturally impossible to do the same task up to the very end.
It is possible to have other decompositions (of the 7 040 squares) than decomposition in types. I show here 2 decompositions in sets of intermediate squares. 6.1 Decomposition with a given basis
You can make a review of the 7 040 squares with a given basis, the first one for example. Each square generates an intermediate square, and this intermediate square generates a set of squares by tabulation with the first basis. The 7 040 squares can then be distributed in sets of disjointed intermediate squares. For each set, you can define an elementary square and search isomorphic sets (by transformations and permutations). You find 9 elementary squares with the first basis (the numbers hereafter are those of my classical program of enumeration, which is a reduced/32 program):
You find that the numbers of squares in the 9 elementary sets are 576 and its divisors (64, 24, 16, 12, 8 and 4). You haven't all the divisors. With the second basis, you find also sets of 32 squares. The 7 040 squares of order 4 can be decomposed in elementary sets of q squares, q being a divisor of (n!)2. It is possible to have other decompositions with the 5 other basis. 6.2 Decomposition with all the basis at the same time
You can do the same at the beginning but you apply after the 6 basis to each intermediate square. Then you have to choose each elementary square in order to have disjointed sets with the 6 basis. You find 6 elementary squares among the 9 previous elementary squares:
This decomposition is more "symmetrical". You have the same property: the 7 040 squares of order 4 can be decomposed in elementary sets of q squares, q being a divisor of (n!)2.
Finally, you have different ways to generate and to decompose the 7 040 magic squares of order 4: 7.1 Generations
7.2 Decompositions
Maybe, it should be possible to find other generations and decompositions.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||